Créer une courbe
Ligne à main levée
![]()
Cette fonction permet de tracer librement des lignes à l’aide du curseur. Les coordonnées indiquées manuellement permettent de tracer une polyligne continue.
- Indiquez le niveau de précision du tracé (c.-à-d. les coordonnées incrémentales maximales) de la polyligne à créer.
Un incrément correspond à la distance L maximale entre deux points parallèles aux axes de coordonnées (voir schéma ci-dessous).
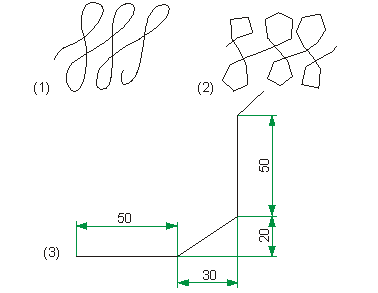
(1) Coordonnées incrémentales max. : 1
(2) Coordonnées incrémentales max. : 10
(3) Incrément - Diagonale et parallèle à l’axe
- Identifiez le point initial de la polyligne.
-
Sélectionnez ensuite le point initial de la ligne à main levée.
- Définissez le point final de la ligne à main levée, puis le point final de la polyligne..
Faites un clic droit pour interrompre la polyligne.
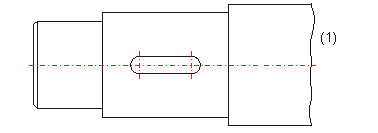
(1) Ligne à main levée
Parabole
Géométrie 2D> Dessiner > Menu déroulant Ligne à main levée > Parabole ![]()
Cette fonction permet de définir un arc de parabole en indiquant 4 points.
-
Indiquez le point initial, l’apex et le foyer de l’arc.
-
Sélectionnez ensuite le point final de l’arc parallèle.
La parabole est déterminée uniquement en fonction de l’apex et du foyer. Le point initial et le point final sont projetés sur la parabole afin de déterminer le début et la fin de l’arc.
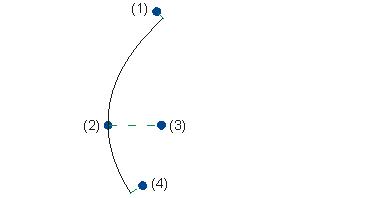
(1) Point initial
(2) Apex
(3) Foyer
(4) Point final
Hyperbole
Géométrie 2D> Dessiner > Menu déroulant Ligne à main levée > Hyperbole![]()
L’hyperbole est une section conique créée lorsque l’angle d’inclinaison formé par l’intersection entre un plan et l’axe d’un cône est inférieur à l’angle d’ouverture du cône de révolution. Dans HiCAD, une hyperbole est définie à partir de 4 points.
- Indiquez le point initial et le point médian.
-
Sélectionnez ensuite un point du diamètre conjugué.
-
Pour terminer, indiquez le point final.
Les trois premiers points permettent de définir une hyperbole équilatère unique sur laquelle le point final est projeté. Les diamètres conjugués sont définis de la même façon que ceux d’une ellipse.
Courbe via équation vectorielle
Géométrie 2D> Dessiner > Menu déroulant Ligne à main levée > Équation vectorielle ![]()
Cette fonction permet de tracer des polylignes à partir d’équations paramétriques vectorielles.
Indiquez une équation pour chacune des coordonnées X et Y dépendantes de T, deux équations de cercle par exemple :
X=F(T)=50*cos(T)
Y=F(T)=20*sin(T)
- Indiquez la valeur initiale et l’incrément de T, par exemple :
1er point de T= 0.00
Incrément de T: 1.00 10
La valeur de l’incrément détermine la précision du tracé de la polyligne.
- Indiquez la valeur finale de T, par exemple :
T=360
Les équations suivantes permettent d’obtenir une ellipse.
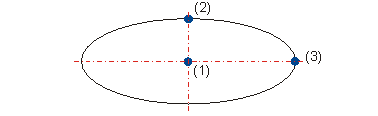
(1) X = 0, Y = 0
(2) X = 0, Y = 20
(3) X = 50, Y = 0
Utilisez les équations suivantes pour créer une spirale :
- X = F(T)= 40*T/360*cos(T)
Y = F(T)= 40*T/360*sin(T)
- Valeur initiale et incrément de T :
1er point de T=0.00
Incrément de T: 1.00 10
- Indiquez une valeur finale de 900.
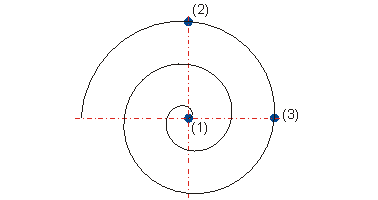
(1) X = 0, Y
= 0
(2) X = 0, Y
= 40
(3) X = 40, Y
= 0

Nouvelle ligne-élément (2D) • Créer une spline (2D) • Modifier une spline (2D)
