Dérivation de splines
vous avez la possibilité de dériver des splines à partir de chaînes de segments. La spline se retrouve des suites de la dérivation sur la chaîne d'arêtes d'origine.
Les courbes de spline ont la propriété de suivre exactement, avec une modification minimale des courbures, les points d'interpolation ou de les dépasser de part et d'autre de la façon aussi lise que possible. Les algorithmes de calculs des courbes de spline appartiennent aux procédés d'interpolation les plus efficaces.
Lors des fonctions indiquées ci-dessus, HiCAD vérifie si la chaîne d'arêtes choisie comporte des courbes. Si c'est le cas, un message correspondant s'affiche alors, par exemple :
En confirmant la question par Oui, seuls les points initial et final des droites seront alors pris en compte pour la création de la spline. L'illustration suivante montre un exemple de la sorte : une spline Akima a été dérivée à partir de l'esquisse de gauche, arc inclus.
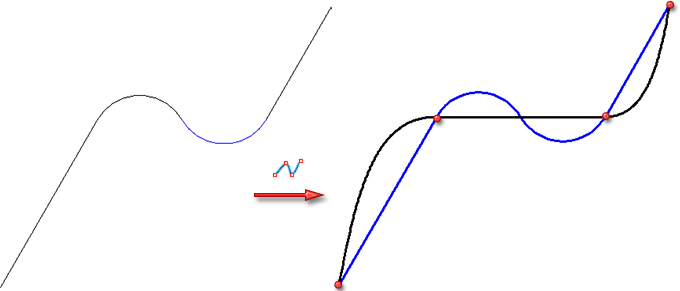
En cliquant sur Non, vous mettez fin à la fonction sans dériver la spline.
Pour convertir ces chaînes de segments de manière à ce que les splines puissent en être directement dérivées, vous pouvez choisir entre les options suivantes :
- Utiliser la fonction Diviser, Avec nombre
. Indiquez ici le nombre adéquat de segments et cochez l'option Convertir les courbes en segments. - Utiliser, pour chaque courbe de la chaîne de segment, la fonction Remplacer ligne
et cochez l'option Remplacer par des segments. - Convertir la chaîne de segments avec la fonction Chaîne d'arêtes -> NURBS
directement dans une spline.
Spline cubique
Esquisse > Main levée > Spline cubique 
La spline cubique est un polynôme du troisième degré qui passe par les points d'interpolation de la chaîne d'arêtes d'origine. Les différents segments/sections du polynôme entre les points d'interpolation touchent les points d'interpolation "sans flexion". On leur attribue une spline lisse, différenciable deux fois de façon continue, sans spécification explicite des conditions tangentielles. Une spline cubique est une interpolation !
Si la chaîne de segments est fermée, la chaîne de la courbe est automatiquement fermée au point commun de départ et de fin avec une transition lisse.
À l'aide de la fonction Spl. cub tangentielle 
, une spline cubique pourra également être créée. Cependant, la 1ère dérivation aux deux points de bord est égale à la direction entre deux points consécutifs de la chaîne de segments d'origine. Cela signifie que les directions de la première et de la dernière arête de la chaîne d'arêtes lissée concordent avec les directions de la première et de la dernière arête de la chaîne d'arêtes d'origine.
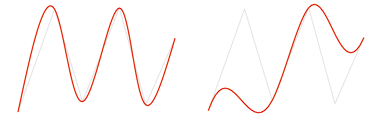
À gauche : spline cubique, à droite : spline cubique, tangentielle
Spline AKIMA
Esquisse > Main levée >
Spline AKIMA 
La spline AKIMA, à la différence de la spline cubique, est locale. Un polynôme du troisième degré y sera également utilisé, ils ne sont différenciables qu'une seule fois de manière continue dans la zone de définition totale. Cela signifie que la nouvelle chaîne d'arêtes n'est définie que par les points d'interpolation situés à proximité immédiate.
Le déplacement d'un point d'interpolation n'affecte que localement la chaîne d'arêtes. En particulier, une plus grande zone en ligne droite est reproduite exactement par de nombreux points d'interpolation dans cette zone. En revanche, la spline cubique présente un comportement plus ondulé.
B-Spline/NURBS
Esquisse > Main levée >
B-Spline/NURBS 
Une b-spline est créée via une séquence ou un maillage de points de Boor, également appelés points de contrôle. La chaîne passant par ces points crée le polygone de Boor ou polygone de contrôle. Une B-spline est locale, c'est-à-dire que les modifications n'ont d'effet que dans une certaine zone de paramètres. Cela permet de coupler un nombre quelconque de fonctions B-spline à une courbe B-spline. Les B-splines ne sont, elles, pas interpolées.
Les courbes NURBS (Non Uniform Rational B-Spline) sont des courbes B-spline rationnelles. Elles offrent un large éventail d'options pour la formation de chaînes de courbes. Les courbes NURBS peuvent se voir attribuer un poids aux points de contrôle. Elles ont une structure similaire aux courbes B-spline. Si le poids aux points de contrôle est égal à 1, la courbe B-spline rationnelle se transforme en courbe B-spline normale. Inversement, chaque courbe B-spline devient une courbe NURBS, si des poids sont attribués à ses points de contrôle.
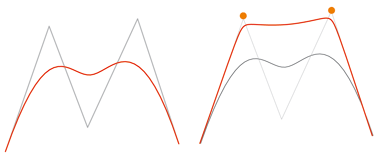
À gauche : B-spline, à droite : les courbes B-splines se sont vu attribuer des poids au niveau des points indiqués. Le résultat est une courbe NURBS.
