Ableiten von Splines
lassen sich aus Streckenzügen Splines ableiten. Der Spline liegt anschließend auf dem Originalkantenzug.
Spline-Kurven haben die Eigenschaft, mit minimaler Krümmungsänderung exakt durch die Stützpunkte zu gehen oder sich möglichst glatt an ihnen "vorbeizuschlängeln". Die Algorithmen zur Berechnung von Spline-Kurven gehören zu den leistungsfähigsten Interpolationsverfahren.
Bei den oben aufgeführten Funktionen wird geprüft, ob der ausgewählte Kantenzug Kurven enthält. Ist dies der Fall, dann wird eine entsprechende Meldung ausgegeben, beispielsweise
Wird diese Meldung mit Ja bestätigt, dann werden für die Erzeugung des Splines nur die Anfangs- und Endpunkte der Geraden berücksichtigt. Die folgende Abbildung zeigt ein solches Beispiel. Aus der linken Skizze ist - inklusive der Bögen - ein Akima-Spline abgeleitet worden.
Bei Wahl von Nein wird die Funktion ohne Ableiten des Splines beendet.
Um diese Streckenzüge so umzuwandeln, dass sich daraus direkt Splines ableiten lassen, stehen Ihnen die folgenden Möglichkeiten zur Verfügung:
- Sie verwenden die Funktion Teilen, Anzahl
. Dort geben Sie eine geeignete Anzahl von Segmenten ein und aktivieren die Option Kurven zu Strecken umwandeln. - Sie verwenden für jede Kurve des Streckenzuges die Funktion Linien ersetzen
ersetzen und aktivieren dort die Option Ersetzen durch Strecken. - Sie wandeln den Streckenzug mit der Funktion Kantentzug -> NURBS
direkt in einen Spline um.
Kubischer Spline
Skizze > Freih... >
Kubischer Spline 
Der kubische Spline ist ein Polynom 3. Grades, das durch die Stützstellen des Originalkantenzuges geht. Die einzelnen Segmente/Abschnitte des Polynoms zwischen den Stützstellen berühren sich an den Stützstellen "ohne Knick". Sie erhalten einen zweimal stetig differenzierbaren, glatten Spline ohne explizite Vorgabe von Tangentialbedingungen. Ein kubischer Spline ist interpolierend!
Wenn der Streckenzug geschlossen ist, wird der Kurvenzug automatisch im gemeinsamen Anfangs- und Endpunkt mit einem glatten Übergang geschlossen.
Mit der Funktion Kubischer Spline tang.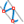 
wird
ebenfalls ein kubischer Spline erzeugt, jedoch ist die 1. Ableitung an
den beiden Randpunkten gleich der Richtung zwischen zwei aufeinander folgenden
Punkten des Original-Streckenzuges. Das bedeutet, dass die Richtungen der
ersten und letzten Kante des geglätteten Streckenzuges mit den Richtungen
der ersten und letzten Kante des Original-Kantenzuges übereinstimmen.
links: Kubischer Spline, rechts: Kubischer Spline, tangential
AKIMA-Spline
Skizze > Freih... >
AKIMA-Spline 
Der AKIMA-Spline ist im Gegensatz zum kubischen Spline lokal. Es werden zwar auch Polynome 3.Grades verwendet, die aber im gesamten Definitionsbereich nur einmal stetig differenzierbar sind. Dadurch wird der neue Kantenzug nur durch die Stützstellen in der unmittelbaren Nachbarschaft bestimmt.
Das Verschieben einer Stützstelle beeinflusst den Kantenzug nur lokal. Insbesondere wird ein größerer geradliniger Bereich über viele Stützstellen in diesem Bereich exakt reproduziert. Im Unterschied dazu zeigt der kubische Spline ein welligeres Verhalten.
B-Spline/NURBS
Skizze > Freih... >
B-Spline/NURBS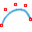 
Ein B-Spline entsteht über eine Folge bzw. ein Netz von de Boor-Punkten, auch Kontrollpunkte genannt. Der Streckenzug durch diese Punkte bildet das de Boor-Polygon bzw. Kontroll-Polygon. Ein B-Spline ist lokal, d. h. Änderungen wirken sich nur in einem gewissen Parameterbereich aus. Somit können beliebig viele B-Spline-Funktionen zu einer B-Spline-Kurve gekoppelt werden. B-Splines sind nicht interpolierend.
NURB-Kurven (Non Uniform Rational B-Spline) sind rationale B-Spline-Kurven. Mit ihnen sind vielfältige weitere Gestaltungsmöglichkeiten von Kurvenzügen möglich. NURB-Kurven können an den Kontrollpunkten mit Gewichten versehen werden. Sie sind analog den B-Spline-Kurven aufgebaut. Beträgt das Gewicht an den Kontrollpunkten 1, geht die rationale B-Spline-Kurve in einen gewöhnlichen B-Spline über. Umgekehrt wird jede B-Spline-Kurve zur NURB-Kurve, wenn ihren Kontrollpunkten Gewichte zugeordnet werden.
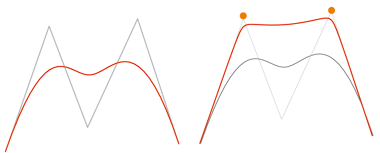
links: B-Spline, rechts: Der B-Spline-Kurve sind an den markierten Punkten Gewichte zugeordnet worden. Das Ergebnis ist eine NURB-Kurve.
