Polyhedral Surface: Smooth Cross-Sections (3-D FFS)

3-D FFS > From c-edges > Connect > Smooth cross-sections

Similar to the Connect cross-sections function, polyhedrons are created by connecting existing cross-sections; however, the cross-sections are smoothed here. Allowed are cross-sections with equal and unequal numbers of points.

1. First, specify the wall thickness.
2. For closed, planar cross-sections you can then determine the treatment of base and top surface.
3. Specify the number of edges for the cross-section.

4. Select the smoothing method:

   Polygon, control point-oriented

   The points of the smoothed cross-section lie on the original cross-section. Their distribution is according to the original corner points.

   Polygon, equidistant

   The points of the smoothed cross-section lie on the original cross-section. Their distribution is even, insofar as the edges of the smoothed cross-section are approximately of the same length.

   Cubic spline

   The points of the smoothed cross-section lie on a cubic spline, the control points of which are the points of the original cross-section.

   Cubic spline, tangential

   Same as cubic spline, but with one difference: the directions of the first and the last edge of the smoothed cross-section coincide with the direction of the first and the last edge of the original cross-section.

   Akima spline

   The points of the smoothed cross-section lie on an Akima spline.This spline type reproduces larger linear areas, via many control points, significantly better than the cubic spline, which would produce a wavier representation.

In the image shown below, the cross-section (1) has been smoothed with the cubic spline method (smoothed cross-section (2)).

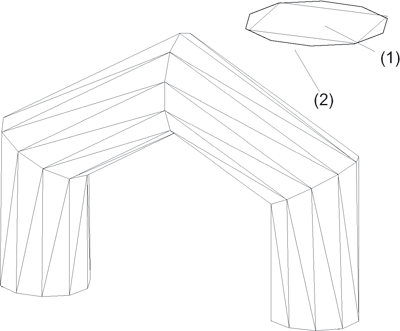
(1) Original cross-section, (2) smoothed cross-section

Method: Cubic spline; Base and top surface: Open; Number of edges for cross-section: 10

Interpolate Cross-Sections (3-D FFS) • Overview of Functions (3-D FFS) • Polyhedral Surfaces (3-D FFS)