Create Curves (2-D)

Freehand line

2-D Geometry > Draw > Freehand line

This function allows you to draw freehand with the cursor. The specified coordinates are implemented in a contiguous polyline.

1. Enter the resolution precision (max. coordinate increment) of the polyline to be generated.
   An increment is the max. distance L between two points parallel to the coordinate axes (see graphic).

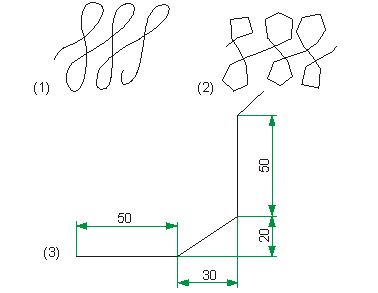
(1) Max. coordinate increment: 1
(2) Max. coordinate increment: 10
(3) Axially parallel and diagonal increment

1. Identify the start point of the polyline.
2. Now choose the start point of the freehand line.
3. Define the end point of the freehand line and then the end point of the polyline.

Use the right mouse button to interrupt the polyline.

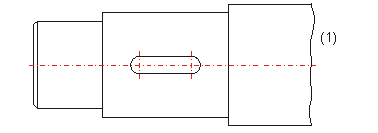
(1) Freehand line

(5) Calculated end point

Parabola

2-D Geometry > Draw > Freehand line > Parabola

This function enables you to define a parabolic arc via 4 points.

1. Specify the start point, vertex and focal point.
2. Choose the end point of the parabolic arc.

The parabola is uniquely defined by the vertex and focal point. The start and end points are projected onto the parabola and used to limit the arc.

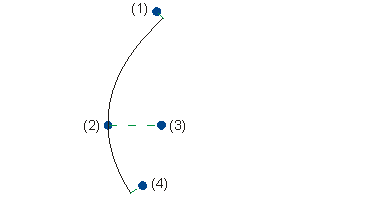
(1) Start point
(2) Vertex
(3) Focal point
(4) End point

Hyperbola

2-D Geometry > Draw > Freehand line > Hyperbola

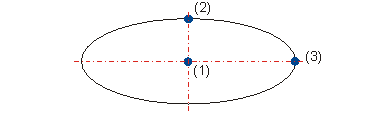
The hyperbola is a conic section that is created when the angle of intersection between intersecting plane and intersected conic axis is smaller than the aperture angle of the double cone. You define a hyperbolic arc via 4 points in HiCAD.

1. Specify the start point and the midpoint.
2. Choose a point on the conjugated diameter.
3. Specify an end point.

A hyperbolic branch is uniquely defined by the first three points, the end point being projected onto it. The conjugated diameters are defined in the same way as those of an ellipse.

Curve via vector equation

2-D Geometry > Draw > Freehand line > Curve via vector equation

You use this function to construct polylines based on vectorial parametric equations.

1. Specify an equation for each of the x- and y-coordinates depending on T, e.g. two circle equations:
   X=F(T)=50*cos(T)
   Y=F(T)=20*sin(T)
2. Specify the initial value and the increment for T, e.g.
   1st point for T=0.00
   Increment for T: 1.00 10
   The number of increments reflects the precision of the polyline.
3. Specify the final value for T, e.g.
   T=360
   You obtain an ellipse for the specified equations.

(1) X = 0, Y = 0
(2) X = 0, Y = 20
(3) X = 50, Y = 0

You generate a helix with the following equations

1. X = F(T)= 40*T/360*cos(T)
   Y = F(T)= 40*T/360*sin(T)
2. Initial value and the increment for T
   1st point for T=0.00
   Increment for T: 1.00 10
3. Specify 900 as the final value.

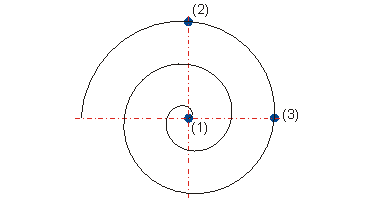
(1) X = 0, Y = 0
(2) X = 0, Y = 40
(3) X = 40, Y = 0

New Graphical Elements (2-D) • Create Splines (2-D) • Edit Splines (2-D)