Teil bewegen, Verschieben + drehen
verschiebt und dreht das aktuelle Objekt durch Angabe des Verschiebevektors und der Drehung

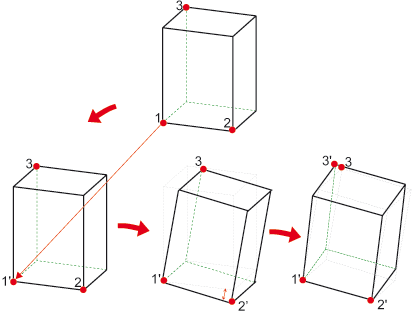
Teil bewegen, über drei Passpunkte
verschiebt und dreht das aktuelle Objekt durch Angabe von "Passpunktpaaren"
 Beispiel
Beispiel