Points médians, centres et centres de gravité

Point médian (milieu)

Point médian (milieu) ,

L'option Milieu d'une ligne (M) détermine le point médian d'une ligne-élément qui se trouve à proximité de la position actuelle du curseur. Pour les arcs de cercle, le point sera déterminé de façon à ce que l'arc soit défini par deux arcs de longueur identique.

Cette option ne peut être utilisée pour les cercles et les ellipses complets.

L'option Milieu entre 2 points (M2) détermine le point médian de deux points quelconques.

Centre (Z)

Centre  I

Cette option détermine le point médian d'un cercle, d'une ellipse ou d'un arc.

Centre d'un cercle polyédrique (ZP)

Centre d'un cercle polyédrique

Dans la 2D

Tout d'abord, HiCAD cherche une ligne qui se trouve à proximité de la position actuelle du curseur. Ensuite, est cherchée l'arête de jonction avec l'angle le plus grand. Le point d'intersection de la médiatrice de ces deux lignes se trouve au centre du cercle polyédrique.

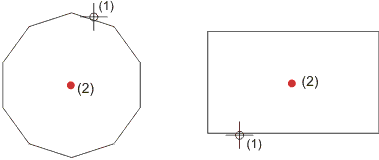
(1) Position du curseur, (2) Point trouvé

Dans la 3D

Tout d'abord, HiCAD cherche l'arête qui se trouve à proximité de la position actuelle du curseur, puis l'arête de jonction avec l'angle de plus grand. Le point d'intersection de la médiatrice de ces deux arêtes s'y applique.

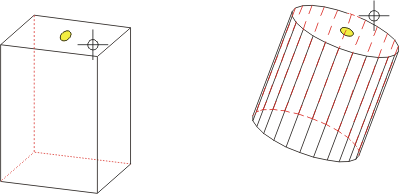
= Position actuelle du curseur, = Point trouvé

Centre de gravité d'une surface (SP)

Centre de gravité I

Ici sera déterminé le centre de gravité d'une surface.

Ne peut être identifié que le centre de gravité d'une surface calculable. Il est impératif que la surface soit composée pour cela d'une polyligne fermée.

Centre de gravité d'un corps (SK)

Centre de gravité de solide

Avec cette option, vous déterminez le centre de gravité d'un corps. Vous identifiez un corps en saisissant son nom.

Options de point en bref