Lisser une chaîne d'arêtes
Esquisse > Main levée > Lisser --> Chaînes de segments 
Une nouvelle chaîne d'arêtes sera ici créée par lissage d'une chaîne d'arêtes existante. Le lissage s'effectue par des procédés mathématiques appropriés qui opèrent soit par interpolation, soit par approximation. Les arcs de cercle seront, à cette occasion, approximés par des polygones.
- Identifiez la chaîne d'arêtes de votre choix.
- Saisissez le nouveau nombre d'arêtes.
- Spécifiez le type de spline en choisissant le procédé de lissage.
|
Procédés de lissage |
|
|---|---|
|
|
Polygone, orienté par point d'interpolation La chaîne d'arêtes d'origine sera lissée par un nouveau polygone. Tous les points d'interpolation de la nouvelle chaîne d'arêtes se trouvent sur les arêtes de la chaîne d'arêtes d'origine. La distance relative entre les points de la chaîne d'arêtes d'origine est respectée dans la mesure du possible. |
|
|
Polygone, équidistant Comme ci-dessus, mais les points de la nouvelle chaîne d'arêtes lissée ont des distances équidistantes (égales) dans l'espace paramétrique de la spline. |
|
|
Spline cubique La spline cubique "classique" est un polynôme du troisième degré qui passe par les points d'interpolation. Les différents segments/sections du polynôme entre les points d'interpolation touchent les points d'interpolation sans flexion. Comme la première et la deuxième dérivation sont continues, le déplacement d'un point d'interpolation influence l'ensemble du trajet de la chaîne d'arêtes. |
|
|
Spline cubique tangentielle Comme ci-dessus, mais la première dérivation aux deux points du bord est égale à la direction entre le 1er et le 2ème ou le (n-1)ème et le nème point de la chaîne d'arêtes d'origine. Cela signifie que les directions de la première et de la dernière arête de la chaîne d'arêtes lissée sont identiques aux directions de la première et de la dernière arête de la chaîne d'arêtes d'origine. |
|
|
Spline AKIMA Contrairement à la spline cubique, la spline d'Akima est locale. Bien que des polynômes du troisième degré soient également utilisés, ils ne peuvent être différenciés qu'une seule fois de manière continue dans la zone de définition totale. Cela signifie que la nouvelle chaîne d'arêtes n'est définie que par les points d'interpolation situés à proximité immédiate. Le déplacement d'un point d'interpolation n'affecte que localement la chaîne d'arêtes. En particulier, une zone rectiligne plus grande est reproduite exactement par de nombreux points d'interpolation dans cette zone, tandis que la spline cubique présente un comportement plus ondulé. |
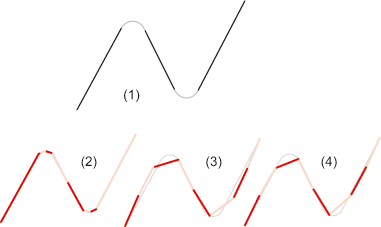
(1) Originale avec 5 arêtes, (2) Polygone orienté par point d'interpolation avec 8 arêtes, (3) Spline cubique, (4) Spline AKIMA
La nouvelle chaîne d'arêtes se trouve exactement sur la chaîne d'arêtes d'origine.
