Chaîne d'arêtes depuis équation vectorielle
Équation vectorielle
Esquisse > Main levée > Équation vectorielle 
Ici, les points d'interpolation seront reliés entre eux par des segments. Pour construire la chaîne d'arêtes, pour chacun des composants X, Y et Z séparément, soit sera spécifiée une équation paramétrique avec le paramètre T, soit sera identifiée une chaîne d'arêtes dont la coordonnée X, Y ou Z aura été appliquée.
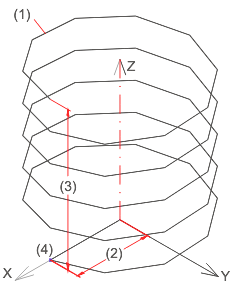
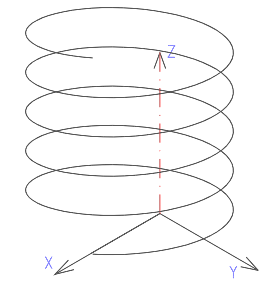
Hélice approximée avec 5 spires, 50 segments et angle initial 0 (entre nombre de points et axe X)
(1) Segment, (2) Rayon moyen de la spire, (3) Hauteur, (4) Nombre de points
Vous devez spécifier chacune des équations pour les composants X, Y et Z l'un après l'autre en fonction de T.
Les paramètres suivants sont pertinents pour l'hélice :
|
r |
Rayon moyen de la spire |
|
a1 |
Nombre de spires |
|
t1 |
Hauteur de l'hélice |
|
i1 |
Nombre de points (=Nombre de segments+1) |
|
w |
Angle initial |
On obtient ainsi l'angle au centre du segment : a=a1*360/i1
Pour l'hélice, T peut être défini comme un incrément dans la direction de l'axe Z.
T=t1/i1, ![]() =a2*T avec a2=a1*360/t1
=a2*T avec a2=a1*360/t1
Si un angle initial w est pris en compte, on obtient les équations vectorielles suivantes:
X(T)=r*cos(w + ![]() ), Y(T)=r*sin(w +
), Y(T)=r*sin(w +
![]() ), Z(T)=T
), Z(T)=T
Ensuite, la portée et l'incrément doivent être précisés pour T, par exemple :
Valeur initiale=0, Incrément=t1/i1, Valeur finale=t1
Vous pouvez également identifier des chaînes d'arêtes dont les positions X/Y/Z sont utilisées à la place d'une formule pour X/Y/Z. Pour ce faire, vous devez vous assurer du même nombre de points et de l'orientation des chaînes d'arêtes. Les chaînes d'arêtes sont traitées comme des chaînes de segments (polylignes) dans ce cas, c'est-à-dire que seuls les points de départ et d'arrivée sont pris en compte.
Cette méthode permet de faire la moyenne des chaînes d'arêtes et de les créer à partir de brouillons. Il est généralement intéressant de combiner les équations paramétriques et la portée dans une macro HiCAD, ce qui permet de faire varier les valeurs des paramètres d'entrée.
REM C O R P S
START 102
REM C O R P S 8=nouveau corps
OPTION 8 102
REM Valeurs par défaut pour les variables plus option de correction
%r:= 10
var %r Moitié du diamètre moyen de la spire
%a1:= 5
var %a1 Nombre de spires
%t1:= 100
var %t1 Hauteur
if t1<0.001 then
%t1:=1
ifend
%i1:= 10
var %i1 Nombre de points
if i1<1 then
%i1:= 10
ifend
%w:= 0
var %w Angle initial
%a2:= a1*360/t1
REM CREER CORPS S5=corps vide
OPTION 8 103
STRING 0
REM K Ö R P E R 1=Modifier corps
OPTION 1 102
REM PARAMETRE CORPS 1=Points/Chaine d'aretes
OPTION 2 106
OPTION 12 137
REM X = F(T) =
STRING r*cos(w+a2*t)
REM Y = F(T) =
STRING r*sin(w+a2*t)
REM Z = F(T) =
STRING t
REM 1er point pour T = :
REAL 0
REM Incrément pour T :
REAL t1/i1
REM Point final pour T = :
REAL t1
OPTION ESC
OPTION ESC
Les lignes qui sont générées automatiquement lors de la création de la macro sont en majuscules, les lignes éditées en minuscules.
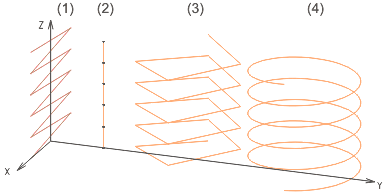
L'illustration ci-dessous montre des hélices pour différentes valeurs d'entrée qui ont été créées avec la macro :
|
Variante |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
|
Moitié du diamètre de la spire |
50 |
50 |
50 |
50 |
|
Nombre de spires |
5 |
5 |
5 |
5 |
|
Hauteur |
100 |
100 |
100 |
100 |
|
Nombre de segments |
10 |
5 |
20 |
300 |
|
Angle initial |
0 |
90 |
180 |
0 |
![]() La variante 2 est "dégénérée" en une chaîne d'arêtes droite de 5 segments (les points délimitent les segments), la variante 1 en une ligne en zig-zag, la variante 4 montre une hélice très bien approximée de 300 segments.
La variante 2 est "dégénérée" en une chaîne d'arêtes droite de 5 segments (les points délimitent les segments), la variante 1 en une ligne en zig-zag, la variante 4 montre une hélice très bien approximée de 300 segments.
Équation vectorielle circulaire
Esquisse > Main levée > Équation vectorielle circulaire 
À la différence de la fonction Équation vectorielle, 2 arcs de cercle qui se superposent tangentiellement seront ici calculés à chacun des points d'interpolation.
Les données pour l'équation vectorielle peuvent être - à l'exception du paramètre w - appliquées de la même façon à l'équation vectorielle circulaire. Il en résulte alors les équations vectorielles suivantes :
X(T)=r*cos(![]() ), Y(T)=r*sin(
), Y(T)=r*sin(![]() ),
Z(T)=T
),
Z(T)=T

