C-Edge via Vector Equation (Sketch)

You can also use vector equations to define composite edges, with the support points being connected with lines oder circular arcs , depending on the respective function.
 

Vector equation

Sketch > Draw > Freehand > Vector equation

The support points are connected by means of lines here. To construct the composite edge, for each of the x-, y- and z-components separately either a parametric equation with parameter T is specified or a composite edge the x-, y- or z-coordinate of which is adopted is identified.

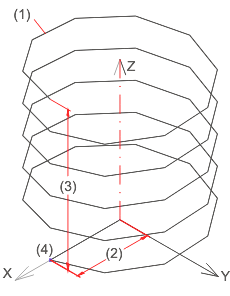
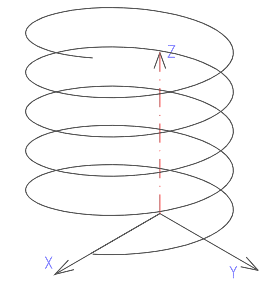
Approximated helices with 5 windings, 50 segments and start angle 0 (between number of points and x-axis)
(1) Segment, (2) Average winding diameter, (3) Height, (4) Number of points

You need to specify each of the equations for the x-, y and z-component in turn, depending on T.

The following parameters are relevant for the helix:

This gives rise to the central angle of the segment: a=a1*360/i1

For the helix T can be defined as an increment in the direction of the z-axis.

T=t1/i1, =a2*T with a2=a1*360/t1

If a start angle w is taken into account, the following vector equations result:

X(T)=r*cos(w + ), Y(T)=r*sin(w + ), Z(T)=T

Next, the scope and the increment need to be specified for T, e.g..

Initial value=0, increment=t1/i1, end value=t1

You can also identify composite edges the x/y/z-positions of which are used instead of a formula for x/y/z. In so doing, you need to make sure of the same number of points and the orientation of the composite edges. Composite edges are treated like polylines in this case, i.e. only the start and end points are considered.

This method allows composite edges to be averaged and to be created from drafts. It is usually worthwhile to combine the parametric equations and the scope in a HiCAD macro, thus enabling the values for the input parameters to be varied.

Macro for helix creation

REM B O D Y

START 102

REM B O D Y 8=nw body

OPTION 8 102

REM Default values for the variables plus correction option

%r:= 10

var %r Half average turn diameter

%a1:= 5

var %a1 Number of turns

%t1:= 100

var %t1 Height

if t1<0.001 then

%t1:=1

ifend

%i1:= 10

var %i1 Number of points

if i1<1 then

%i1:= 10

ifend

%w:= 0

var %w Start angle

%a2:= a1*360/t1

REM CREATE BODY S5=dummy body

OPTION 8 103

STRING 0

REM B O D Y 1=Process body

OPTION 1 102

REM BODY PARAMETER 1=Points/composite edge

OPTION 2 106

REM 3D COMPOSITE EDGE 5=Vector equation

OPTION 12 137

REM X = F(T) =

STRING r*cos(w+a2*t)

REM Y = F(T) =

STRING r*sin(w+a2*t)

REM Z = F(T) =

STRING t

REM 1st point for T = :

REAL 0

REM Increment for T :

REAL t1/i1

REM End point for T = :

REAL t1

OPTION ESC

OPTION ESC

The lines that are generated automatically during macro creation are in upper case, the edited lines in lower case.

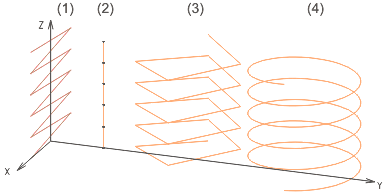
The image below shows helices for different input values that have been created with the macro:

Variant 2 has "degenerated" into a straight-line composite edge consisting of 5 segments (points bound the segments), variant 1 into a zigzag line and variant 4 shows a very well approximated helix of 300 segments.

Circular vector equation

Sketch > Draw > Freehand > Circular vector equation

In contrast to the Vector equation function, 2 circular arcs that merge into one another tangentially are calculated at each of the support points here.

You can apply the specifications for the vector equation in the same way to the circle vector equation - except for parameter w. This gives rise to the following vector equations: X(T)=r*cos( ), Y(T)=r*sin( ), Z(T)=T Y(T)=r*sin(), Z(T)=T

3-D Sketch (3-D) • Sketch Functions (3-D)