Derivation of Splines (Sketch)

You can use the

• Cubic spline
• AKIMA Spline and
• B-Spline/NURBS

functions to derive splines from existing polylines. The feature of spline curves is that they can pass through the support points exactly with minimum change of curvature or "wind past" them as smoothly as possible. The algorithms for calculating spline curves are amongst the most powerful interpolation methods.

Notes:

• The spline lies subsequently on the original composite edge. To approximate splines, select Sketch > Others > Process C-edge > Approximation.
• Select Sketch > Others > Edge Settings to change the precision of the spline representation.

Cubic spline

Sketch > Draw > Freehand > Cubic spline

The cubic spline is a third-degree polynomial which passes through the support points of the original composite edge. The individual segments/sections of the polynomial between the support points touch the support points "without bend". They are assigned a twice continuously differentiable smooth spline without explicit specification of tangential conditions. A cubic spline is interpolating!

If the polyline is closed, the continuous curve is automatically closed in the common start and end point with a smooth transition.

The Tangential cubic spline function is also used to create  a cubic spline. However, the 1st derivation at the two edge points is equal to the direction between two consecutive points of the original polyline. This means that the directions of the first and last edge of the smoothed polyline are identical to the first and last edge of the original composite edge.

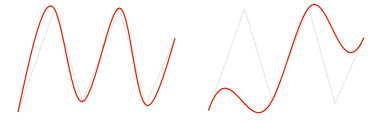
Left: Cubic spline; Right: Tangential cubic spline

AKIMA spline

Sketch > Draw > Freehand > Akima spline

Unlike the cubic spline, the Akima spline is local. Although third-degree polynomials are also used, they are only once continuously differentiable in the total definition area. This means that the new composite edge is only defined by the support points in the immediate vicinity.

Moving a support point only affects the composite edge locally. In particular, a larger straight-line area is reproduced exactly via many support points in this area. By contrast, the cubic spline displays more wavy behaviour.

B-Spline/NURBS

Sketch > Draw > Freehand > B-spline/NURBS

A B-Spline is created via a sequence or a mesh of de Boor points, also called control points. The polyline through these points creates the de Boor polygon or control polygon. A B-spline is local, i.e. changes only have an effect in a certain parameter area. This enables any number of B-spline functions to be coupled to a B-spline curve. B-splines are not interpolating

NURB curves (Non Uniform Rational B-splines) are rational B-spline curves. They offer a wide range of options for the shaping of continuous curves. NURB curves can be assigned weights at the control points. They have a similar structure to B-spline curves. If the weight at the control points is 1, the rational B-spline curve changes to a normal B-spline. Conversely, every B-spline curve becomes a NURB curve if weights are assigned to its control points.

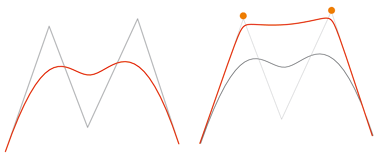
Left: B-spline, Right: The B-spline curve has been assigned weights at the highlighted points. The result is a NURB curve.

3-D Sketch (3-D) • Sketch Functions (3-D)