Sketch > Freehand... > Smooth c-edge 
A new composite edge is created by smoothing an existing composite edge. Smoothing is performed using suitable mathematical methods which work by interpolation or approximation. Circular arcs are approximated by means of polygons.
|
Smoothing procedures |
|
|---|---|
|
|
Polygon, support-point oriented The original composite edge is smoothed by means of a new polygon. All support points of the new composite edge lie on the edges of the original composite edge. The relative point distance of the original composite edge is complied with as far as possible. |
|
|
Polygon, equidistant As above, but the points of the new smoothed composite edge have equidistant (equal) distances in the parametric space of the spline. |
|
|
Cubic spline The "classic" cubic spline is a third-degree polynomial which goes through the support points. The individual segments/sections of the polynomial between the support points touch the support points without bend. As the 1st and 2nd derivation are continuous, moving a support point influences the entire composite edge path. |
|
|
Cubic spline, tangential As above, but the 1st derivation at the two edge points is equal to the direction between the 1st and 2nd or (n-1)th and nth point of the original composite edge. This means that the directions of the first and last edge of the smoothed composite edge are identical to the directions of the first and last edge of the original composite edge. |
|
|
AKIMA spline Unlike the cubic spline, the Akima spline is local. Although third-degree polynomials are also used, they are only once continuously differentiable in the total definition area. This means that the new composite edge is only defined by the support points in the immediate vicinity. Moving a support point only affects the composite edge locally. In particular, a larger straight-line area is reproduced exactly via many support points in this area, while the cubic spline displays more wavy behaviour. |
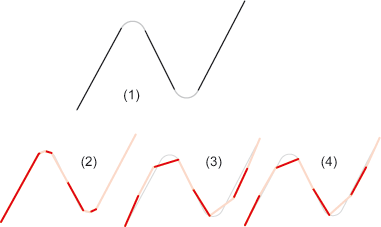
(1) Original with 5 edges, (2) polygon support point-oriented with 8 edges, (3) cubic spline, (4) AKIMA-spline
![]() The new composite edge lies exactly on the original composite
edge.
The new composite edge lies exactly on the original composite
edge.

3-D Sketch (3-D) • Sketch Functions (3-D)
|
© Copyright 1994-2018, ISD Software und Systeme GmbH |