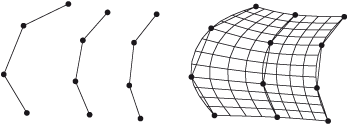
Fläche aus Streckenzuggerüst

3D-FFF > Aus Kantenzügen > Fläche aus Streckenzuggerüst

Mit den Funktionen dieses Menüs leiten Sie Freiformflächen aus einem Gerüst ab. Ein Gerüst ist eine Sammlung von Kantenzügen mit gleicher Anzahl von Einzelkanten und gleicher Orientierung. Die Kantenzüge müssen demselben Kantenzugteil angehören. Ein Gerüst kann insbesondere mit der Funktion Querschnitt verlegen erzeugt werden.

Die entstehenden Freiformflächen können Sie mit den Funktionen unter Freiformflächen bearbeiten modellieren und manipulieren. Zur Änderung der Flächendarstellung, beispielsweise zur Bestimmung der Anzahl der Parameterlinien in u- und v-Richtung, verwenden Sie Funktionen unter Einstellungen > Sonstiges.

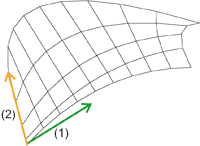
Parameterlinien in u- (1) und v-Richtung (2)

Bei der Erzeugung einer Freiformfläche aus einem Gerüst ist grundsätzlich Folgendes zu beachten:

So gehen Sie vor:

  1. Aktivieren Sie das Teil mit dem Gerüst und rufen Sie dann die Funktion auf.
  2. Im Feld Gerüst wird der Name des aktiven Teils angezeigt. Geben Sie im Feld Name den Teilenamen für die Freiformfläche ein.
  3. Wählen Sie dann die Art der Erzeugung durch Punkteoder als Kontrollpunkte, indem Sie das entsprechende Optionsfeld aktivieren und dann in der zugehörigen Listbox den gewünschten Eintrag wählen.
  4. Sind die Kantenzüge des Gerüstes geschlossen, dann können Sie unter Flächenverband/Volumen festlegen, wie die Grund- und Deckfläche des erzeugten Bauteils behandelt werden sollen. Werden sowohl die Grund- als auch die Deckfläche geschlossen, dann entsteht ein Solid. Damit kann es beispielsweise gebohrt oder geschnitten werden.
  5. Klicken Sie auf Vorschau, wenn Sie die Freiformfläche vor der Übernahme in die Konstruktion kontrollieren wollen.
  6. Mit OK übernehmen Sie die Freiformfläche.

Durch Punkte

Die Parameterlinien der erzeugten Freiformfläche sind Splines.

Kubischer Spline

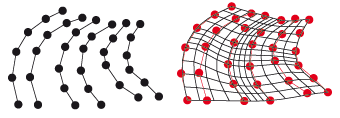
Die Parameterlinien der hier erzeugten Freiformfläche sind kubische Splines, d. h. sie sind zweimal stetig differenzierbarer und glatt, ohne Tangentialbedingungen und interpolierend.

Kubischer Spline – tangential

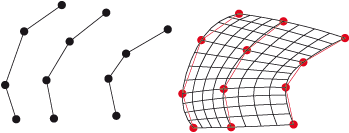
Auch hier sind die Parameterlinien der erzeugten Freiformfläche kubische Splines, jedoch mit Tangentialbedingung. Die Tangente wird jeweils ermittelt durch die Richtung des zweiten Punktes zum vorletzten Punkt eines Kantenzuges. Das Gerüst muss hier aus mindestens 6 Kantenzügen bestehen.

Kubischer Spline – Bessel

Hier werden die Splines, aus denen die Freiformfläche abgeleitet wird, nach dem Bessel-Verfahren bestimmt. Die Randtangenten werden dabei geschätzt als Tangenten einer 3 Punkte interpolierenden Parabel.

Akima-Spline

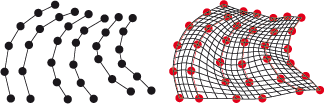
Die Parameterlinien der Freiformfläche sind Akima-Splines. Diese sind im Unterschied zu kubischen Splines lokal. Es werden zwar auch Polynome 3. Grades verwendet, die aber im gesamten Definitionsbereich nur einmal stetig differenzierbar sind. Dadurch wird der neue Kantenzug nur durch die Stützstellen in der unmittelbaren Nachbarschaft bestimmt. Da der Akima-Spline geteilte Geraden und Ebenen exakt darstellen kann, zeigt er in solchen Fällen ein weniger welliges Verhalten als der kubische Spline.

Als Kontrollpunkte

Hier entsteht eine B-Spline-Fläche über eine Folge bzw. ein Netz von de-Boor-Punkten, auch Kontrollpunkte, genannt. Ein B-Spline ist lokal, d. h. Änderungen wirken sich nur in einem gewissen Parameterbereich aus. Eine B-Spline-Fläche wird zu einer NURB-Fläche, wenn man ihren Kontrollpunkten Gewichte zuordnet, deren Wert ungleich 1 ist. Wählen Sie den B-Spline-Grad. Ist der Grad zu hoch, dann liefert HiCAD eine entsprechende Meldung.

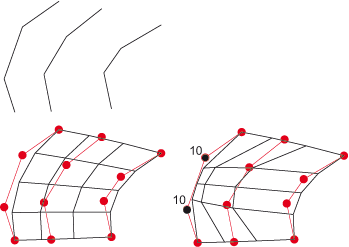
Oben: Gerüst, unten links: B-Spline, Unten rechts: NURB

Querschnitte interpolieren (3D-FFF) • Funktionsübersicht (3D-FFF) • Freiformflächen