Kurven erzeugen
Freihandlinie
![]()
Diese Funktion erlaubt Ihnen das freihändige Zeichnen mit dem Cursor. Die angegebenen Koordinaten werden in einem zusammenhängenden Linienzug umgesetzt.
- Geben Sie die Auflösungsfeinheit (Max. Koordinateninkrement) des zu erzeugenden Linienzugs ein.
Ein Inkrement ist der max. Abstand L zweier Punkte parallel zu den Koordinatenachsen.
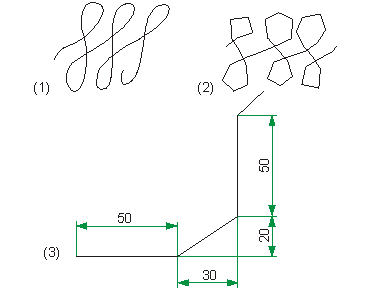
(1) Max. Koordinateninkrement:
1
(2) Max. Koordinateninkrement:
10
(3) Achsparalleles und diagonales Inkrement
- Identifizieren Sie den Anfangspunkt des Linienzuges.
- Wählen Sie nun den Anfangspunkt der Freihandlinie.
- Bestimmen Sie den Endpunkt der Freihandlinie und danach den Endpunkt des Linienzuges.
Mit der rechten Maustaste wird der Linienzug unterbrochen.
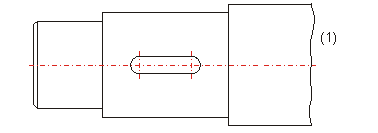
(1) Freihandlinie
Parabel
2D Geometrie > Zeichnen > PullDown-Menü Freihandlinie > Parabel ![]()
Mit dieser Funktion können Sie einen Parabelbogen über 4 Punkte definieren.
- Geben Sie den Anfangs-, Scheitel- und Brennpunkt an.
- Wählen sie den Endpunkt des Parabelbogens.
Die Parabel ist durch den Scheitel- und Brennpunkt eindeutig festgelegt. Der Anfangs- und der Endpunkt werden auf die Parabel projiziert und zur Begrenzung des Bogens verwendet.
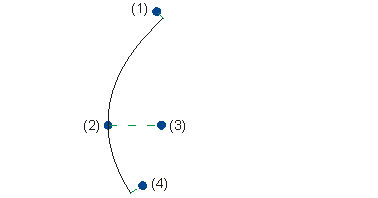
(1) Anfangspunkt
(2) Scheitelpunkt
(3) Brennpunkt
(4) Endpunkt
Hyperbel
2D Geometrie > Zeichnen >PullDown-Menü Freihandlinie > Hyperbel ![]()
Die Hyperbel ist ein Kegelschnitt, der entsteht, wenn der Schnittwinkel zwischen schneidender Ebene und geschnittener Kegelachse kleiner als der Öffnungswinkel des Doppelkegels ist. Einen Hyperbelbogen definieren Sie in HiCAD über 4 Punkte.
- Geben Sie den Anfangs- und den Mittelpunkt an.
- Wählen sie einen Punkt auf dem konjugierten Durchmesser.
- Geben Sie einen Endpunkt an.
Durch die ersten drei Punkte ist ein Hyperbelast eindeutig festgelegt, der Endpunkt wird auf diesen projiziert. Die konjugierten Durchmesser sind analog denen einer Ellipse definiert.
Kurve über Vektorgleichung
2D Geometrie > Zeichnen > PullDown-Menü Freihandlinie > Vektorgleichung ![]()
Mit dieser Funktion konstruieren Sie Linienzüge auf der Grundlage von vektoriellen Parametergleichungen.
- Geben Sie je eine Gleichung für die X- und die Y-Koordinate in Abhängigkeit von T an, z. B. zwei Kreisgleichungen:
X=F(T)=50*cos(T)
Y=F(T)=20*sin(T)
- Geben Sie den Anfangswert und die Schrittweite für T an, z. B.
1. Punkt bei T=0.00
Schrittweite für T: 1.00 10
Die Anzahl der Schrittweite gibt die Feinheit des Linienzuges wieder.
- Geben Sie den Endwert für T an, z. B.
T=360
Für die angegebenen Gleichungen erhalten Sie eine Ellipse.
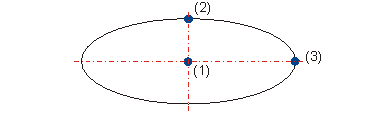
(1) X = 0, Y = 0
(2) X = 0, Y = 20
(3) X = 50, Y = 0
Eine Spirale erzeugen Sie mit den folgenden Gleichungen
- X = F(T)= 40*T/360*cos(T)
Y = F(T)= 40*T/360*sin(T)
- Anfangswert und die Schrittweite für T
1. Punkt bei T=0.00
Schrittweite für T: 1.00 10
- Geben Sie für den Endwert 900.
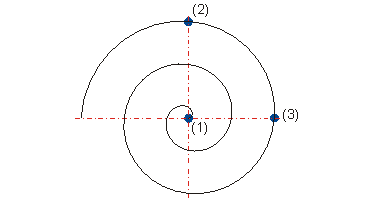
(1) X = 0, Y
= 0
(2) X = 0, Y
= 40
(3) X = 40, Y
= 0

Linienelement neu (2D) • Splines erzeugen (2D) • Splines bearbeiten (2D)
